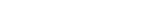The phenomenon of synchronization is found in many natural and artificial systems, from firefly flashing to the synchronization of two pendulum clocks hanging from a wall.
Hydrodynamic interactions also play a role in synchronized motions of coupled oscillators in fluids. Therefore, understanding the mechanism will facilitate development of applications in fluid mechanics. For example, synchronization phenomenon in two-phase flow will benefit the design of future microfluidic devices, allowing spatiotemporal control of microdroplet generation without additional integration of control elements, according to the research team.
Professor Joonwoo Jeong and his research team in the Department of Physics at UNIST discovered that the system can act as a coupled oscillator, notably showing spontaneous in-phase synchronization of droplet breakup, using a characteristic oscillation of adjacent interfaces between two immiscible fluids in a microfluidic platform.
Figure 1. The different modes of droplet breakup at the double T junction. (a) In-phase and out-phase synchronization of droplet breakup. (b) State diagram of the synchronization mode with effective dimensionless numbers.
In addition to the frequent encounter of the out-of-phase synchronization mode in droplet generation from two interfaces of immiscible fluids, the research team discovered the regime of in-phase synchronization with phase-locking in contrast to the nonsynchronous regime from the weak coupling.
“The discovery of these overlooked regimes in the microfluidic T junction completes the state diagram of coupled oscillators accompanying small noises,” noted the research team. “Our experiments and theoretical model elucidate that the coupling depends on the distance between the interfaces which governs the forces acting on the interfaces, and also explain the transition between the in-phase and out-of-phase modes of droplet breakup.”
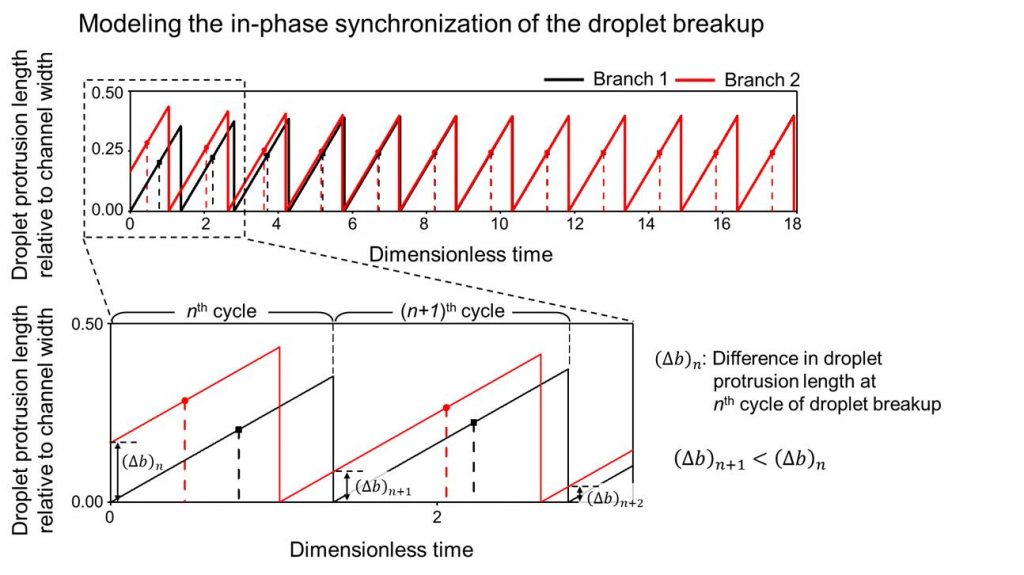
Figure 2. Development of the in-phase synchronization model from experimental parameters. (Top) Model calculation showing the stability of the in-phase synchronization mode. The evolution of the protrusion heights shows how the initially nonsynchronous state converges to the state of perfect in-phase synchronization. (Bottom) Expanded view of the data shown in the dashed box in (c), showing the variables to explain the stabilizing mechanism of the in-phase synchronization; the definition of each variable is written in the main text. Each cycle is defined by one droplet-breakup sequence from branch 1, as indicated by brackets on top of the graph. The difference in b between two branches, (Δb)n where n denotes the order of the cycle, decreases with each cycle, eventually leading to the in-phase synchronization.
The research team expects that the microfluidic system of oscillating interfaces described in this work serves as an instructive model for studying hydrodynamic interactions leading to synchronization, with adjustable coupling strength using confinement and flow rates. They also noted that “For applications, the microfluidic technology capable of inducing such stable synchronization or desynchronization of droplet generation provides a new avenue for the valveless control of delivery and triggered reactions of materials in microdroplet formats.”
This study has been jointly participated by Professor Joo Hun Kang from the Department of Biomedical Engineering at UNIST. The findings of this research have been published in the online version of Nature Communications on October 15, 2020. This study has been supported by the Basic Science Research Program and the President’s Postdoctoral Fellowship Program through the National Research Foundation of Korea (NRF) and the Ministry of Science and ICT (MSIT).
Journal Reference
Eujin Um, Minjun Kim, Hyoungsoo Kim, et al., “Phase synchronization of fluid-fluid interfaces as hydrodynamically coupled oscillators,” Nature Communications, (2020).