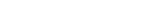한 사회의 자원은 한정돼 있다. 남보다 더 많이 가지려면 경쟁이 필수다. 하지만 혼자만 잘 살겠다고 욕심을 부리다간 집단 전체가 파국을 맞을 수 있다. 그렇다면 어떻게 자원을 배분해야 함께 잘 사는 사회를 이룰 수 있을까.
사회학자나 경제학자가 연구할 것 같은 심오한 질문에 수학자가 답변을 내놨다. 개인과 사회의 에너지를 표현하는 전기 회로로 사고실험을 진행한 결과다. 여기에 따르면 개인의 다양성이 보장되고, 서로간의 연결이 획일적이지 않으며, 경쟁이 존재하는 사회가 영속성이 높았다.
김필원 자연과학부 교수는 ‘최대전력 게임(Maximum Power Game)’이라는 수학적 모델로 사회의 흥망을 살피는 연구를 진행했다. 최대전력 게임은 사회적 자원과 에너지의 배분 문제를 전기회로라는 최소한의 물리적 모형에서 구현한 뒤 ‘게임이론(Theory of games)’을 적용해 해석한 모델이다. 게임이론은 경쟁상대의 반응을 고려해 자신의 최적 행위를 결정해야 하는 상황에서 의사결정 행태를 연구하는 경제학 및 수학이론이다.
김필원 교수는 “경제학에서는 ‘공유지의 비극(The tragedy of the commons)’이라는 비유를 통해 개인들이 사적 이익만 추구하면 집단 전체가 파국을 맞을 수 있다고 지적해왔다”며 “이런 고전적 게임이론을 확장시켜 ‘어떤 사회의 구조에서 개인의 이기적 노력이 자연스럽게 집단 전체의 높은 효율로 연결될 수 있는가’를 탐구하고자 했다”고 연구 배경을 밝혔다.
‘전기회로=사회’, ‘개인=가변저항’… 사회구조에 따른 자원분배 균형 밝혀
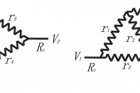
최대전력 게임에서 개인은 하나의 전기저항으로 표현된다. 이들은 최대의 일률을 내기 위해 더 많은 전력을 소모하기 위해 노력한다. 사회에서 더 많은 것을 얻기 위해 경쟁하는 개인과 같다. 이런 저항들은 다양한 구조에서 서로 연결된 전기회로가 될 수 있는데, 이를 하나의 사회로 생각할 수 있다. 사회를 저항과 전압으로 이뤄진 회로로 단순화한 것이다.
그림1. 다양한 저항을 나타낸 그림. 이들은 한 사회에서 자원(전력)을 얻으려 경쟁하는 개인으로 생각할 수 있다.
하나의 저항은 자신을 통과하는 전압과 전류에 반응해 값을 조절한다. 이 값은 전기회로 안에서 다른 저항들과 얽혀 있다. 개인의 선택(저항 변화)이 다른 사람과 사회(전기회로)에 어떤 영향을 주는지 분석하는 모델로 활용할 수 있는 것이다.
김 교수는 “최대전력 게임에서는 1대 1의 자원분배를 다루던 고전적 게임이론을 여럿 대 여럿(multo-to-multi) 게임으로 확장시킬 수 있다”며 “회로구조에 따라 에너지 분배 균형이 어떻게 바뀌는지 분석함에 따라 고전적 게임이론을 물리적‧사회적으로 확장시킬 수 있는 방법론이라는 걸 확인했다”고 설명했다.
모두 경쟁하면 지속 못해… ‘중재’나 ‘희생’ 있어야 존속
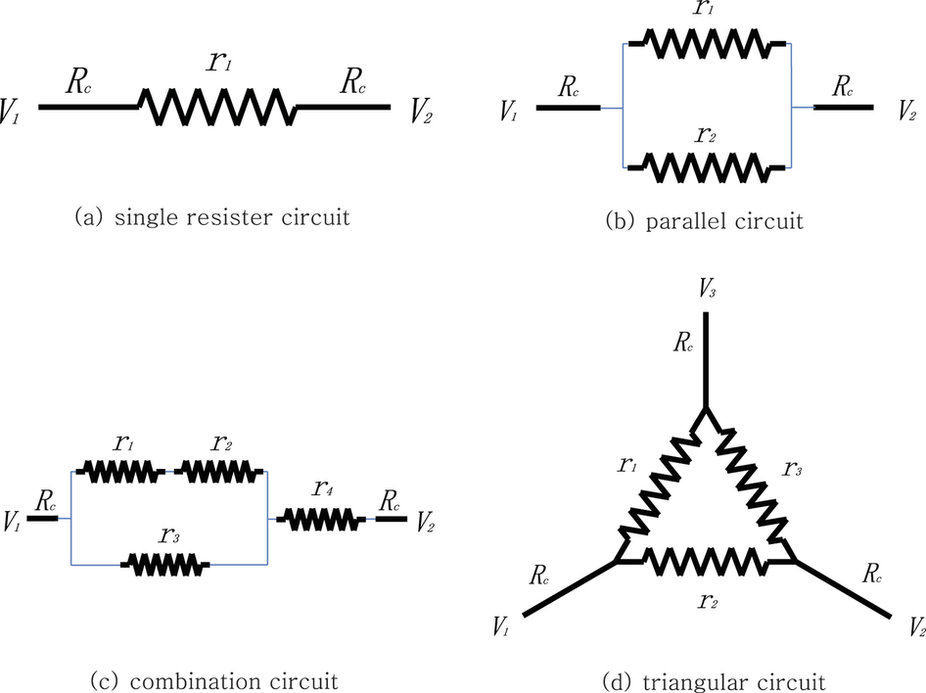
김 교수는 우선 이기적인 개인들이 마음껏 경쟁하는 사회를 전기회로로 구현했다. 저항을 직렬이나 병렬, 혹은 그들의 조합으로 만든 것이다. 이렇게 연결하면 각 저항은 계속 올라가면서 많은 전력을 확보하기 위해 경쟁한다. 저항이 계속 올라가면 결국 부도체가 돼 전기가 흐르지 않게 된다. 회로가 망가지는 것이다. 사회로 치면 개인들의 무한한 경쟁이 사회의 작동을 멈추게 하는 것으로 생각할 수 있다.
그림 2. 직렬과 병렬을 조합해 만든 전기회로. 이런 회로에서는 저항이 계속 올라가는 경쟁이 심해지면 결국은 회로가 망가지게 된다. ‘죄수의 딜레마’나 ‘공유지의 비극’처럼 개인의 이익만 추구하는 결과 파국을 맞는 것에 비유할 수 있다.
김 교수는 “이런 현상은 고전적 게임이론에서 유명한 ‘죄수의 딜레마 게임(prisoner’s dilemma game)’나 ‘공공재 게임(public good game)’과 유사하다”며 “사회구조가 단순할 때 개인 간의 경쟁은 모두의 패배를 낳고 사회적으로 낭비가 극대화된다”고 해석했다.
이런 파국을 피하기 위한 방법은 간단하다. 단순한 구조에서 벗어나 일정한 비정형성을 허용하는 것이다. 실제로 전기저항을 마름모꼴로 배치하자 회로가 멈추지 않고 작동했다. 이때 한 가지 조건이 있다. 마름모꼴의 가운데에 놓인 저항은 전력을 얻지 못하고 ‘희생’하는 것이다. 김 교수는 이 현상을 두고 “사회, 국가가 멈추지 않고 계속 어어 나가려면 누군가의 희생이나 중재가 필요함을 보여준다”고 풀이했다.
그림3. 직렬이나 병렬이 아닌 새로운 형태로 만든 전기회로는 저항이 올라가도 망가지지 않았다. 이런 구조에서는 희생되는 부분이 생기게 마련이다.
능력과 개성 존중해야… 게으른 사람도 ‘존재 이유’ 있어
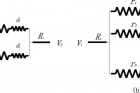
전기회로 속 저항 값을 다르게 한 경우의 결과도 흥미롭다. 이 차이는 개인들의 효율성 차이로 볼 수 있다. 김 교수는 회로 속 각 저항에 서로 다른 ‘고정저항’을 붙여봤다. 고정저항은 개인이 살아가는 데 반드시 필요하지만 손실되는 에너지를 뜻한다. 부지런한 사람은 고정저항이 작고, 게으른 사람은 고정저항이 크다.
각 저항에 서로 다른 고정저항을 넣은 뒤 게임이론에 적용하자 직렬, 병렬로 연결돼도 회로가 망가지지 않았다. 김 교수는 “이는 뒤처지는 사람도 쓸모가 있음을 보여주는 모형”이라며 “고정저항 값의 차이는 개인이 가진 능력과 개성의 차이로 볼 수 있는데, 이런 차이가 경쟁을 의미 있게 만들 수 있다”고 설명했다.
그림4. r은 저항, d는 고정저항을 나타낸다. 고정저항을 붙일 경우 직렬이나 병렬로 연결된 회로고 망가지지 않고 작동했다. 사회 구성원의 능력이나 효율의 차이가 중요한 이유가 드러나는 대목이다.
그는 이어 “만약 게임에서 아주 높은 효율을 가진 상대와 경쟁해야 한다면 그와 마찬가지로 고효율이 되는 것은 서로에게 도움이 안 된다”며 “부지런한 경쟁자와 겨루는 상대가 게으른 사람일 경우 둘과 사회 전체에게 이익이 돌아간다”고 덧붙였다.
이는 조직에서 업무효율이 떨어지더라도(고정저항이 큰 저항을 의미) 내치면 안 되는 이유와도 연결된다. 모두가 1등을 차지하는 사회는 존재하지 않는다. 누군가는 2등, 3등의 위치에 있어야 사회가 존속하는 것이다. 1등만 바라보고 지나치게 경쟁하는 사회가 오히려 효율이 떨어지는 역설적인 상황이 전기회로 실험에서도 그대로 드러났다.
똑같은 배분은 NO!… 적당한 경쟁이 발전 이끌어
이번에는 수많은 전압과 저항을 연결한 뒤 경쟁 없이 중앙에서 최적의 분배를 조율하는 전기회로를 만들어봤다. 이런 사회는 강력한 중앙정부가 개인에게 자원을 할당하는 공산주의 체제에 빗댈 수 있다.
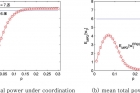
경쟁 없는 전기회로의 전체 에너지는 7.25로 계산됐다. 반면 적절한 구조에서 각 저항이 서로 경쟁한 회로 전체의 에너지는 5.95였다. 여기까지는 중앙집권식이 더 효율적인 것으로 보인다. 하지만 중앙집권식의 경우 작은 변화만 있어도 전체 에너지가 순식간에 무너졌다. 반면 경쟁 있는 회로에서는 값이 변하거나 충격이 가해져도 적절한 에너지를 유지했다.
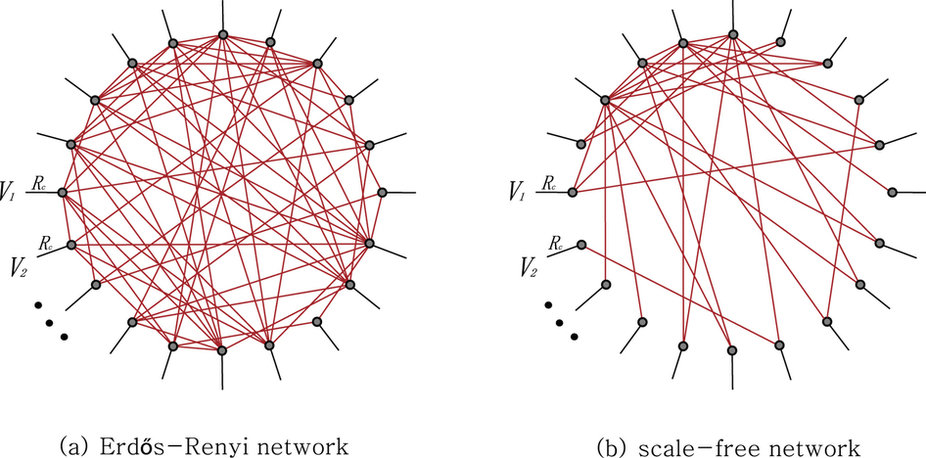
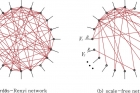
그림5. (a)는 일정한 규칙을 주고 무작위로 전기회로를 연결한 모습이고, (b)는 척도 없는 네트워크로 연결된 전기회로망이다. (a)는 중앙집권식으로 통제한 사회, (b)는 자연스러운 경쟁이 유발되는 사회에 비유할 수 있다. 후자의 경우 전체 에너지도 크게 차이가 나지 않으면서도 존속이 가능했다.
김 교수는 “전기회로망에서는 저항의 연결이 ‘척도 없는 네트워크(scale–free network)’를 이룰 때 전체적으로 효율이 높아졌다”며 “저항들이 집단 경쟁을 통해 평균적으로 높은 전력 생산량을 보인 것”이라고 설명했다.
척도 없는 네트워크는 대푯값이나 평균이 없는 연결 상태를 뜻한다. 사람의 키나 몸무게처럼 어떤 대표성을 띠는 숫자로 모이지 않고 작은 확률이라도 무수히 존재해 대표적인 구조나 성질을 한마디로 표현할 수 없는 것이다. 이는 자연스러운 경쟁이 존재하는 사회로 볼 수 있다.
김 교수는 “최대전력 게임을 통한 여러 실험은 결국 다양성하고 복잡한 구조를 가진 사회에서 경쟁이 이뤄질수록 개인의 이기적인 노력이 자연스럽게 집단 전체의 효율을 높이게 된다는 결론을 준다”고 말했다.
전기회로를 이용한 사고실험으로 사회적 자원을 배분하는 방법을 연구한 이번 논문은 사이언티픽 리포트(Scientific Reports) 3월 8일자로 게재됐다. 지난 2월 25일자 <매일경제신문>에서는 ‘사이언스엔(Science&)’ 코너에 이 연구를 미리 소개하기도 했다.
